analytic_z-spectra-cw-2pool
Table of Contents
Analytic Z-spectra water, CEST - cw
Here you find analytic solutions of the Bloch-McConnell equations describing Z-spectra.
This is the R1ρ-model as published in Zaiss and Bachert (2013), NMR Biomed., 26: 507–518. doi: 10.1002/nbm.2887. 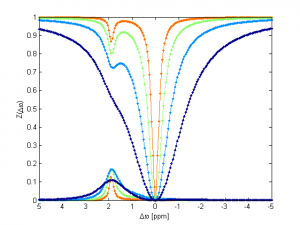
It is a very lean code to give you a tool illustrating the principal behaviour of a CEST effect and its interaction with the direct water saturation.
Dowload zipped Matlab implementations here or find the package on github.com/cest-sources/Z-cw
Tutorial
The code
BATCH_Z_cw
First the pool parameters are defined in the parameter struct P:
%% SETUP %pool system parameters %water pool A P.R1A=1/3; % longitudinalrelaxation rate [s^-1] P.R2A=2; % transversal relaxation rate [s^-1] P.dwA=0; %deltaW_A in [ppm] %CEST pool B P.fB=0.001; % proton fraction: [water protons]/[CEST agent protons] P.kBA=200; % exchange rate [s^-1] P.dwB=1.9; % (chemical shift) deltaW_B in [ppm} P.R2B=30; % transversal relaxation rate [s^-1]
Now the CEST sequence parameters are defined
% sequence parameters P.Zi=1; % Z initial, in units of thermal M0, Hyperpol.: 10^4 P.FREQ=300; % [MHz] I use ppm and µT, therefore gamma=267.5153; P.B1=2; % [µT] P.tp=5; % pulse duration = saturation time [s] P.xZspec= [-5:0.1:5]; % ppm
Now the function Z_cw(P) is called and plotted:
figure(32), plot(P.xZspec,Z_cw(P),'r-') ; hold on;
function Z_cw(P)
analytic_z-spectra-cw-2pool.txt · Last modified: 2021/10/11 13:22 (external edit)

